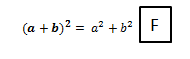Problemas con ecuaciones de segundo grado

Revisa los problemas siguientes:

Problema 1


Problema 2



En el segundo video, el expositor plantea un método diferente a los trabajados en clase (para los ejercicios 1; 2 y 4). ¿De qué manera resolverías tú estos problemas? Explica tu procedimiento.
(En el cuarto problema cambia el valor de la hipotenusa por 5, en lugar de 6)

Fracciones

Fracciones

Integrantes:

Andrea Gazzo

Alessandra Rodriguez-Mariategui

Alessandra Takashima

Mariana Vasquez

Isabella Perez



Repaso para el examen progresivo

1: Inecuaciones

BIEN RESUELTO

BIEN RESUELTO

BIEN RESUELTO

2: Ecuaciones

   BIEN RESUELTO

 

En una juguetería donde se venden bicicletas y triciclos, Percy dijo: “hay 60 llantas”. Oscar agregó: “Hay 5 bicicletas más que triciclos, ¿cuántas bicicletas hay?

Bicicletas: x

Triciclos:   y

BIEN RESUELTO. SOLO FALTA DAR LA RESPUESTA DEL NÚMERO DE BICICLETAS (X): 15 BICICLETAS

3: Productos notables

EN LA c) ES 0,09m2

4: Factorizacion

EN LA PRIMERA FALTA SEGUIR FACTORIZANDO

EN LA SEGUNDA HAY ALGO QUE NO CUADRA

EN LA TERCERA FALTA OPERAR LOS PARÉNTESIS. RESPUESTA: (4m - n)(2m + n)

BIEN RESUELTO

Critina Fontenoy, Gabriela Gaber, Belen Gonzalez, Anneliesse Indacochea y Malu Muñoz

productos notables y tirangulo de pascal

                                               

                   

                    b) (x + 20)(x – 4) = x²+16x-80

                   

                     Formula: Producto de dos binomios con un termino común

                    c)   (p³ + 7m)² = p⁶ +14 mp³+49m²

                    Formula: Cuadrado del binomio suma

                   d)  (x³ + 5y)² + (x³ – 5y)² =

                         2x⁶+25y⁴

                         formula: (a+b)² = A²+2ab+b²

                                         Formula 2: (a-b)² =A²-2ab+b²

                   e) (m + 3)² – (m – 3)² =

                       m²+6m+9-(m²-6m+9)

                       m²+6m+9-m²+6m-9

                      12m

                      Formula: (a+b)²= a²+2ab+b²

                                     Formula 2: (a-b)²=a² -2ab+b²

                      f) (x + 2)(x – 2)(x – 5)(x + 5)

                          x²-4+x²-25

                          x⁴-29x²+100

                          Formula: (a+b)(a-b) =a²-b²

 

            

                       h) (b + 1)⁴  

                        b⁴+4b³+6b²+4b+1

                        Formula: producto de un binomio suma

                                       (a+b)²=a²+2ab+b²

                  

              

                      

      

  j) (x⁵y-1,2x)² =

           X¹⁰y²-2x⁵y1,2x+1,44x

           X¹⁰y²-2,4x⁶y+1,44x

           Formula:producto de binomio de una resta

                          (a-b)²=a²-2ab+b²

 

        

        

l)Halla el valor de m²+n²,si mn=3 y m+n=7/2

           M²+n²=(m+n)² = m²+2mn+n²

           Mn=3=m²+6+n²

                 M²+6+N²

           (7/2)²=+6+M²+N²

                  49 - 24/4=M²+N²

           25/4=M²+N²

                      

             

                    

      

Productos Notables (Semana 9-13 de Setiembre)

Productos Notables

Cada producto notable corresponde a una fórmula de factorización. Hay muchas fórmulas entre las que se encuentran las siguientes:


Observación: el primer producto notable se conoce también como el cuadrado del binomio suma; el segundo, como el cuadrado del binomio diferencia; y el tercero, como producto del binomio suma por el binomio diferencia.

Ejercicios
Escribe verdadero (V) o falso (F) en cada afirmación:

Esta afirmación es falsa ya que al resolverla usando la fórmula del cuadrado de la suma de dos términos que sería elevar el primer término al cuadrado más el doble del producto de ambos términos más el segundo término elevado al cuadrado, no te da el resultado dado que era el primer término elevado al cuadrado más el segundo término elevado al cuadrado.

Esa afirmación es falsa ya que usando la fórmula del producto de la suma de dos términos por la resta de los mismos que sería elevar el primer término al cuadrado menos el segundo término elevado al cuadrado no te da el resultado dado.

 

En esta pregunta te piden hallar el área de este cuadrado y que cada lado vale x+2 entonces para hallar el área puedes multiplicar lado x lado o lado elevado al cuadrado ya que sería lo mismo. Si lo elevas al cuadrado podrías usar la fórmula del cuadrado de la suma de dos términos y sería más fácil hallar la respuesta.

 Resuelve:

Para resolverlo debes elevar el primer término al cuadrado menos el segundo término al cuadrado.

Para resolverla primero multiplicamos el primer término por sí mismo porque está elevado al cuadrado. Luego, multiplicamos el primer término por el segundo y después lo multiplicamos por 2. Finalmente, elevamos el segundo término al cuadrado y es así como llegamos al resultado final.

Calcula mentalmente:



Simplifica las siguientes expresiones:

Resuelve: